Introduction
Dans le chapitre précédent, il a été démontré qu'il était facile d'obtenir des situations mathématiques exactes pour les forces exercées par des fluides au repos. En effet, en hydrostatique, seules des forces de pression simples sont impliquées. Lorsqu'un fluide en mouvement est considéré, le problème de l'analyse devient d'emblée beaucoup plus complexe. Il faut non seulement prendre en compte la vitesse et la direction des particules, mais aussi l'influence complexe de la viscosité, qui provoque une contrainte de cisaillement ou de frottement entre les particules en mouvement et aux limites qui les contiennent. Le mouvement relatif possible entre les différents éléments du fluide fait varier considérablement la pression et la contrainte de cisaillement d'un point à un autre selon les conditions d'écoulement. En raison de la complexité du phénomène d'écoulement, une analyse mathématique précise n'est possible que dans quelques cas, parfois peu pratiques du point de vue technique. Il est donc nécessaire de résoudre les problèmes d'écoulement soit par l'expérimentation, soit en formulant des hypothèses simplificatrices suffisantes pour obtenir une solution théorique. Ces deux approches ne s'excluent pas mutuellement, car les lois fondamentales de la mécanique sont toujours valables et permettent l'adoption de méthodes partiellement théoriques dans plusieurs cas importants. Il est également important de déterminer expérimentalement l’ampleur de l’écart par rapport aux conditions réelles résultant d’une analyse simplifiée.
L'hypothèse simplificatrice la plus courante est que le fluide est idéal ou parfait, éliminant ainsi les effets de viscosité complexes. C'est le fondement de l'hydrodynamique classique, une branche des mathématiques appliquées qui a retenu l'attention d'éminents chercheurs tels que Stokes, Rayleigh, Rankine, Kelvin et Lamb. La théorie classique présente de sérieuses limites intrinsèques, mais comme l'eau a une viscosité relativement faible, elle se comporte comme un fluide réel dans de nombreuses situations. De ce fait, l'hydrodynamique classique peut être considérée comme une base précieuse pour l'étude des caractéristiques du mouvement des fluides. Ce chapitre traite de la dynamique fondamentale du mouvement des fluides et sert d'introduction aux chapitres suivants traitant des problèmes plus spécifiques rencontrés en hydraulique du génie civil. Les trois équations fondamentales du mouvement des fluides, à savoir les équations de continuité, de Bernoulli et de quantité de mouvement, sont dérivées et leur signification expliquée. Les limites de la théorie classique sont ensuite examinées et le comportement d'un fluide réel est décrit. L'hypothèse d'un fluide incompressible est retenue.
Types de flux
Les différents types de mouvement des fluides peuvent être classés comme suit :
1.Turbulent et laminaire
2. Rotationnel et irrotationnel
3. Stable et instable
4. Uniforme et non uniforme.
Pompe submersible pour eaux usées
Pompes axiales de la série MVS et pompes mixtes de la série AVS (pompes submersibles pour eaux usées à flux axial vertical et à flux mixte) sont des produits modernes, conçus avec succès grâce à l'adoption de technologies étrangères modernes. Leur capacité est supérieure de 20 % à celle des anciennes pompes et leur rendement est supérieur de 3 à 5 %.

Écoulement turbulent et laminaire.
Ces termes décrivent la nature physique du flux.
En écoulement turbulent, la progression des particules du fluide est irrégulière et leur déplacement semble aléatoire. Chaque particule est soumise à des vitesses transversales fluctuantes, ce qui crée un mouvement tourbillonnaire et sinueux plutôt que rectiligne. Si un colorant est injecté en un point précis, il se diffusera rapidement dans l'écoulement. Dans le cas d'un écoulement turbulent dans une conduite, par exemple, un enregistrement instantané de la vitesse à un endroit précis révélerait une distribution approximative, comme illustré à la figure 1(a). La vitesse stationnaire, telle qu'enregistrée par des instruments de mesure classiques, est indiquée en pointillés, et il apparaît que l'écoulement turbulent se caractérise par une vitesse fluctuante instable superposée à une moyenne temporelle stationnaire.
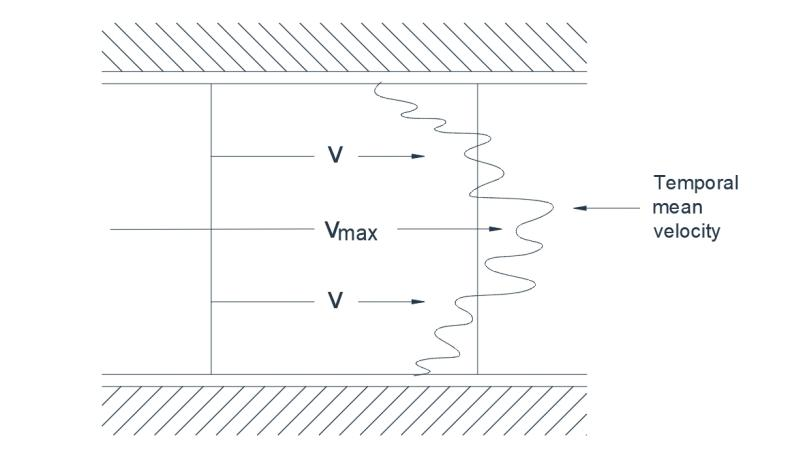
Fig.1(a) Écoulement turbulent
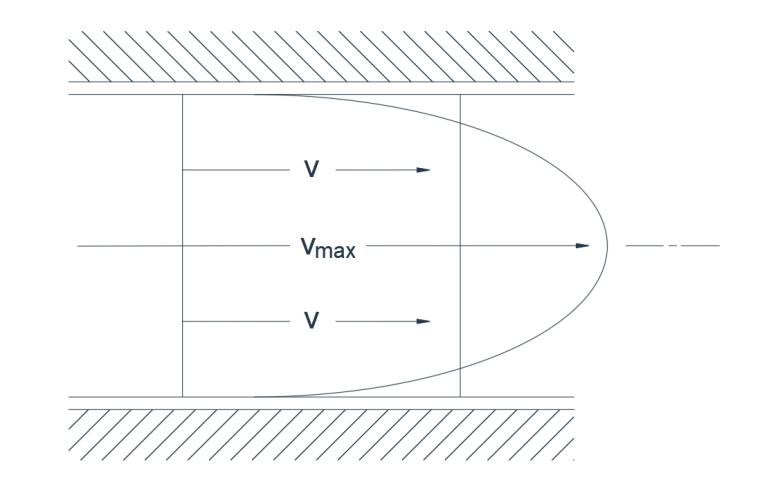
Fig.1(b) Écoulement laminaire
En écoulement laminaire, toutes les particules du fluide suivent des trajectoires parallèles et il n'y a pas de composante transversale de vitesse. La progression ordonnée est telle que chaque particule suit exactement la trajectoire de la particule qui la précède sans déviation. Ainsi, un fin filament de colorant restera tel quel, sans diffusion. Le gradient de vitesse transversale est beaucoup plus important en écoulement laminaire (Fig. 1b) qu'en écoulement turbulent. Par exemple, pour un tuyau, le rapport entre la vitesse moyenne V et la vitesse maximale V max est de 0,5 en écoulement turbulent et de 0,05 en écoulement laminaire.
L'écoulement laminaire est associé à de faibles vitesses et à des fluides visqueux et lents. En hydraulique des pipelines et des canaux ouverts, les vitesses sont presque toujours suffisamment élevées pour assurer un écoulement turbulent, bien qu'une fine couche laminaire persiste à proximité d'une limite solide. Les lois de l'écoulement laminaire sont parfaitement comprises et, pour des conditions limites simples, la distribution des vitesses peut être analysée mathématiquement. En raison de sa nature pulsatoire irrégulière, l'écoulement turbulent a défié tout traitement mathématique rigoureux, et pour la résolution de problèmes pratiques, il est nécessaire de s'appuyer largement sur des relations empiriques ou semi-empiriques.

Pompe à incendie à turbine verticale
Numéro de modèle : XBC-VTP
Les pompes incendie verticales à arbre long de la série XBC-VTP sont des pompes à diffuseurs monocellulaires et multicellulaires, fabriquées conformément à la dernière norme nationale GB6245-2006. Leur conception a également été améliorée en se référant à la norme de l'Association américaine de protection contre les incendies. Elles sont principalement utilisées pour l'alimentation en eau d'extinction d'incendie dans les secteurs de la pétrochimie, du gaz naturel, des centrales électriques, du textile, des quais, de l'aviation, de l'entreposage, des immeubles de grande hauteur, etc. Elles conviennent également aux navires, aux réservoirs maritimes, aux navires de lutte contre les incendies et à d'autres applications.
Écoulement rotationnel et irrotationnel.
L'écoulement est dit rotatif si chaque particule de fluide a une vitesse angulaire autour de son propre centre de masse.
La figure 2a illustre une distribution de vitesse typique associée à un écoulement turbulent au-delà d'une limite rectiligne. En raison de cette distribution de vitesse non uniforme, une particule dont les deux axes sont initialement perpendiculaires subit une déformation avec un faible degré de rotation. La figure 2a illustre un écoulement circulaire.
La trajectoire est représentée, la vitesse étant directement proportionnelle au rayon. Les deux axes de la particule tournent dans le même sens, de sorte que l'écoulement est à nouveau rotatif.
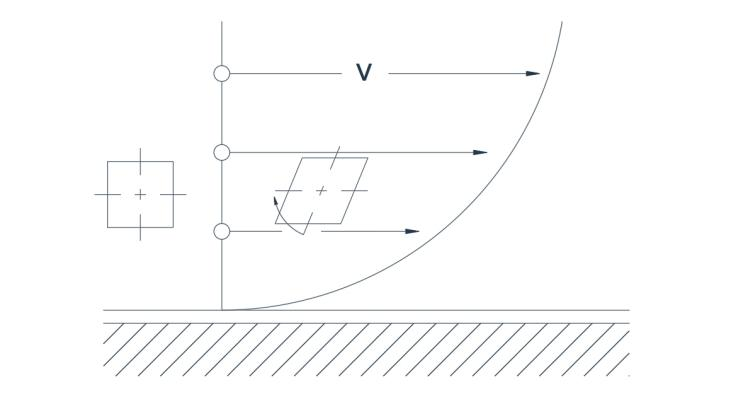
Fig.2(a) Écoulement rotationnel
Pour que l'écoulement soit irrotationnel, la distribution des vitesses adjacentes à la limite droite doit être uniforme (Fig. 2b). Dans le cas d'un écoulement suivant une trajectoire circulaire, on peut montrer que l'écoulement irrotationnel ne se produit que si la vitesse est inversement proportionnelle au rayon. À première vue, la figure 3 semble erronée, mais un examen plus approfondi révèle que les deux axes tournent en sens inverse, de sorte qu'un effet de compensation produit une orientation moyenne des axes inchangée par rapport à l'état initial.
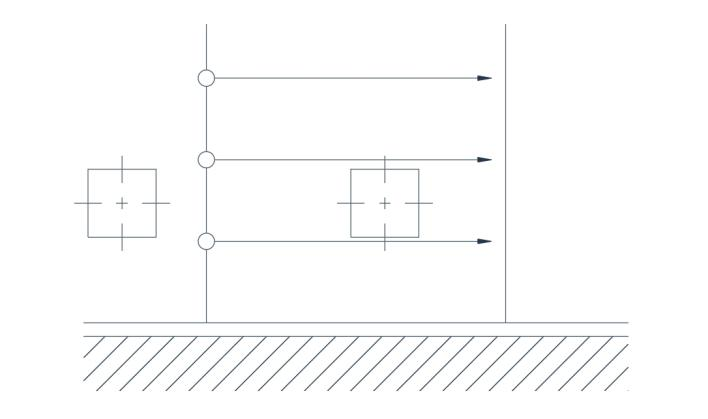
Fig.2(b) Écoulement irrotationnel
Comme tous les fluides possèdent une viscosité, le fluide réel n'est jamais véritablement irrotationnel, et l'écoulement laminaire est naturellement fortement rotationnel. Ainsi, l'écoulement irrotationnel est une condition hypothétique qui ne présenterait d'intérêt académique que si, dans de nombreux cas d'écoulement turbulent, les caractéristiques rotationnelles sont si insignifiantes qu'elles peuvent être négligées. Ceci est pratique car il est possible d'analyser l'écoulement irrotationnel à l'aide des concepts mathématiques de l'hydrodynamique classique évoqués précédemment.
Pompe centrifuge de destination d'eau de mer
Numéro de modèle : ASN ASNV
Les pompes modèles ASN et ASNV sont des pompes centrifuges à volute divisée à double aspiration à un étage et utilisées pour le transport de liquides pour les travaux d'eau, la circulation de climatisation, la construction, l'irrigation, la station de pompage de drainage, la centrale électrique, le système d'approvisionnement en eau industriel, le système de lutte contre l'incendie, le navire, le bâtiment, etc.

Flux régulier et instable.
On dit qu'un écoulement est stationnaire lorsque les conditions en tout point sont constantes dans le temps. Une interprétation stricte de cette définition conduirait à la conclusion qu'un écoulement turbulent n'a jamais été véritablement stationnaire. Cependant, pour le présent exposé, il est plus commode de considérer le mouvement général du fluide comme le critère et les fluctuations erratiques associées à la turbulence comme une influence secondaire. Un exemple évident d'écoulement stationnaire est un débit constant dans une conduite ou un canal ouvert.
En corollaire, il s'ensuit que l'écoulement est instable lorsque les conditions varient dans le temps. Un exemple d'écoulement instable est un débit variable dans une conduite ou un canal ouvert ; il s'agit généralement d'un phénomène transitoire succédant ou suivi d'un débit constant. Autres phénomènes courants
Des exemples de nature plus périodique sont le mouvement des vagues et le mouvement cyclique de grandes masses d'eau dans le flux des marées.
La plupart des problèmes pratiques en génie hydraulique concernent l'écoulement stationnaire. Heureusement, la variable temporelle en écoulement instationnaire complexifie considérablement l'analyse. Par conséquent, dans ce chapitre, l'étude de l'écoulement instationnaire se limitera à quelques cas relativement simples. Il est important de garder à l'esprit, cependant, que plusieurs cas courants d'écoulement instationnaire peuvent être ramenés à l'état stationnaire grâce au principe du mouvement relatif.
Ainsi, un problème impliquant un navire se déplaçant en eau calme peut être reformulé de telle sorte que le navire soit immobile et l'eau en mouvement ; le seul critère de similarité du comportement des fluides est que la vitesse relative soit identique. De même, le mouvement des vagues en eau profonde peut être réduit à la
état stationnaire en supposant qu'un observateur se déplace avec les ondes à la même vitesse.

Pompe de drainage d'eau centrifuge multicellulaire à turbine verticale diesel. Cette pompe de drainage verticale est principalement utilisée pour pomper les eaux usées non corrosives, dont la température est inférieure à 60 °C et dont la teneur en solides en suspension (à l'exclusion des fibres et des gravillons) est inférieure à 150 mg/l. La pompe de drainage verticale de type VTP est intégrée aux pompes à eau verticales de type VTP. La lubrification du tube est assurée par de l'eau, en fonction de l'augmentation et du collier. Elle peut être utilisée pour pomper des eaux usées contenant des particules solides (ferraille, sable fin, charbon, etc.) à des températures inférieures à 60 °C.
Écoulement uniforme et non uniforme.
On dit qu'un écoulement est uniforme lorsque l'amplitude et la direction du vecteur vitesse sont constantes d'un point à l'autre de son trajet. Pour respecter cette définition, l'aire d'écoulement et la vitesse doivent être identiques à chaque section. Un écoulement non uniforme se produit lorsque le vecteur vitesse varie selon l'emplacement, un exemple typique étant l'écoulement entre des limites convergentes ou divergentes.
Ces deux conditions alternatives d'écoulement sont courantes en hydraulique à ciel ouvert, même si, à proprement parler, l'écoulement uniforme étant toujours approché asymptotiquement, il s'agit d'un état idéal qui n'est qu'approché et jamais réellement atteint. Il convient de noter que ces conditions sont spatiales et non temporelles et, par conséquent, dans le cas d'écoulements confinés (par exemple, dans des conduites sous pression), elles sont totalement indépendantes de la nature stationnaire ou instable de l'écoulement.
Date de publication : 29 mars 2024
 sales@tkflow.com
sales@tkflow.com 
